Value Gradient weighted Model-Based Reinforcement Learning
Claas Voelcker, Victor Liao, Animesh Garg, Amir-massoud Farahmand
ICLR 2022 (spotlight paper)
paper, code
With the rise of powerful and flexible function approximation, model-based reinforcement learning (MBRL) has gained a lot of traction in recent years. The core idea of MBRL is intuitive: (a) use the data obtained by online interaction of an agent with its environment, (b) build a surrogate model of this environment, and (c) use this model to improve the agent’s planning capabilities.
 |
A sketch of the DYNA algorithm. The model is used to generate additional data for the RL agent training. |
While intuitive, this approach can start to suffer once we obtain multimodal, high resolution sensory information. In these cases, the agent may be observing more of the world that it needs to for completing its task and creating a predictive model of the full environment may actually be harder than the task at hand itself!
In most MBRL approaches, the environment model is obtained from the maximum likelihood objective, often via a reconstruction loss where the model tries to predict the next observation and agent will encounter from the previous observations and actions. However, if the observation contains many superfluous dimensions, the MLE objective is ineffective, as much of the model capacity is spent on approximating the full complexity of the observation space.
Our key proposal is to regularize the model learning by the sensitivity of the value function for different inputs. Intuitively, if the value function is not influenced by changing the observation, the model is not required to be accurate. To highlight how we arrive at this solution, let’s look at the problem and previous proposals in more detail.
When is a model mismatched?
 |
For a car driving task, it is important to differentiate important from unimportant environment features. While it is very important to predict the likelihood of pedestrians entering the road, the clouds in the sky are just distractions. |
This phenomenon has been termed the “objective mismatch”: the model does not know anything about the task the agent is trying to solve, no information from the task is fed back to the model learning, so the objectives of the agent (“obtaining high reward”) and the model (“achieving low reconstruction error”) do not necessarily align. When trying to solve this problem, we quickly run into a catch-22: one of the core assumptions underlying decision making is that we do not know how to solve the task, otherwise we would not be doing model learning in the first place. We need an accurate model of the environment before we can solve the task, so how can we feed task information back to the model before solving it?
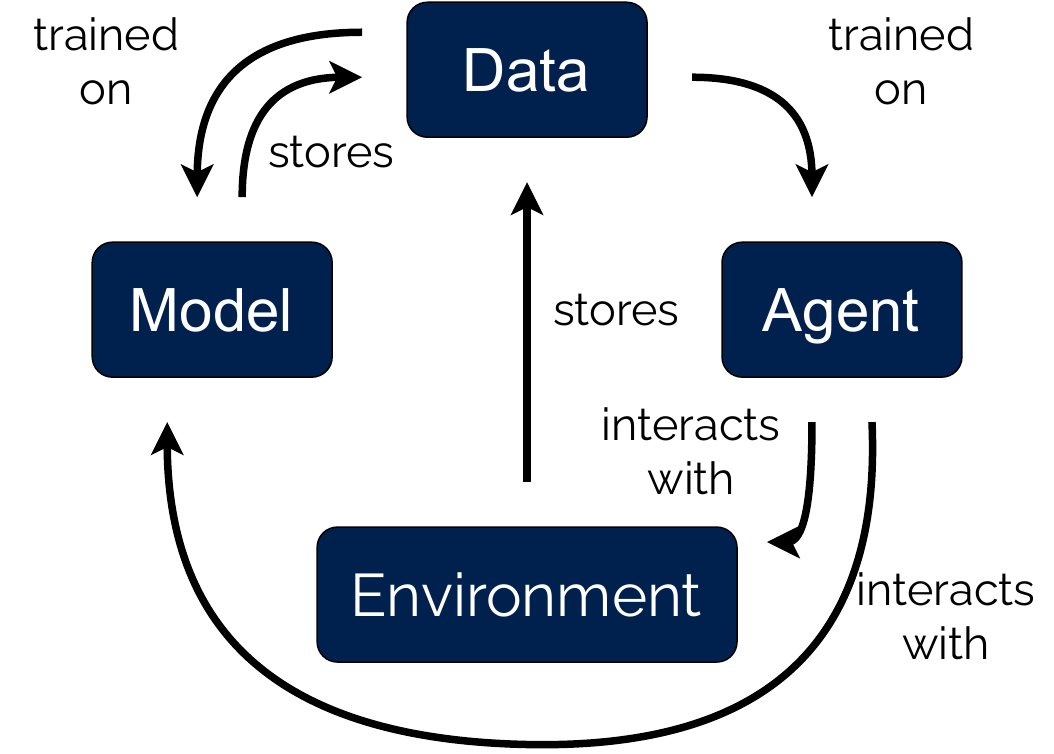
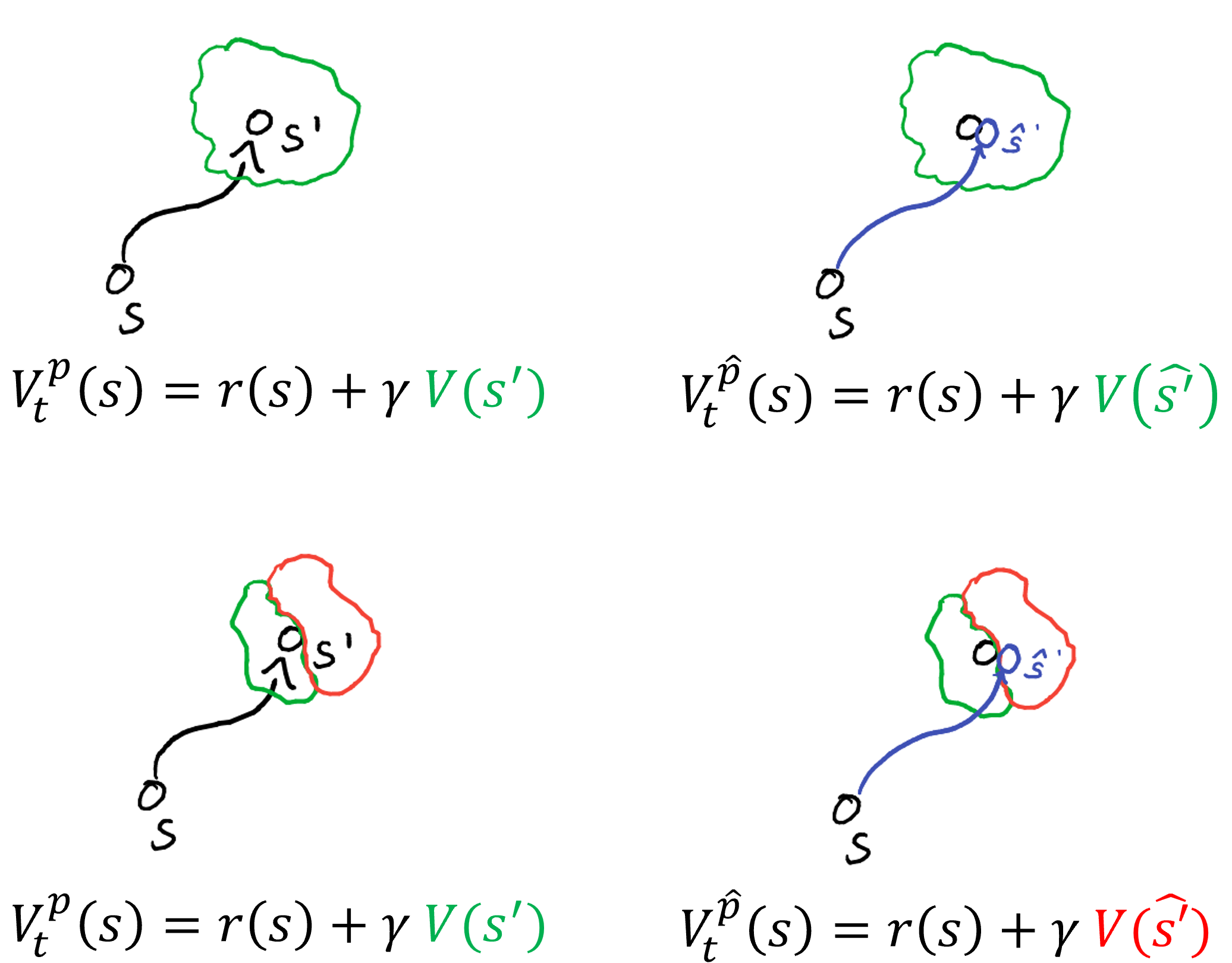 |
On the left side, the model predictions are correct. On the right hand side they are wrong. In the top right image, the model prediction does not lead to a change in the value function prediction, so no error is fed back. In the bottom right corner, the model error leads to a difference in value function, so the error is propagated to the RL algorithm. |
In their papers “Value-aware model learning” and “Iterative value-aware model learning”, Farahmand et al. present two potential solutions to the problem: by analyzing the way in which the model is used in a Dyna algorithm, they show that the model only influences the policy via its value function. This means that even if the model prediction is wrong, as long as the value function prediction aligns with the real environment, the RL agent is not impacted by the model error. Conversely, even if the model only makes a small error, if the value function is very sensitive to small changes in the state space, the resulting value prediction can be very wrong. Following from this observation, Farahmand et al. propose to replace the model learning loss with a loss that measures the difference in value function.
\[\mathcal{L}_V(\hat{p}, p, \mu) = \int \mu(s,a) \bigg|\overbrace{\int p(s'|s,a)V(s')\mathrm{d}s'}^{\text{environment value estimate}} - \overbrace{\int \hat{p}(s'|s,a) V(s') \mathrm{d}s'}^{\text{model value estimate}}\bigg|^2 \mathrm{d} (s,a)\]Does this solve the objective mismatch problem?
Although the theoretical underpinnings of the VAML approach are rigorous, when naively applying the algorithm in practice, two problems quickly become apparent.
(1) In many RL environments, we cannot assume that the state space is fully explored in early iterations, which means that there are many possible states in which we do not have data to learn a value function. However, a function approximation will still assign a value to these points, interpolating from previously seen points in the training set, often resulting in nonsensical values. When the model predicts that a next state is in an unexplored region of the state space, the VAML loss will not penalize it for predicting a completely wrong state if the value functions align. In some cases it can even drive the prediction further into the unexplored regions, simply because it only seeks to find a local optimum of the value function prediction. When the value function is updated, the predictions in the regions of the state space that are not covered by data often change rapidly, which suddenly cause very large value function prediction errors when using model data.
(2) The second problem is the smoothness of the value function and resulting VAML loss. In many common applications, the value function is not convex or smooth, exhibiting plateaus and ridges that make the VAML loss difficult to optimize. In the image below we show the value function of the Pendulum environment. The non-smooth nature of the function shows in the two sharp ridges. When non-smooth value functions are coupled with out-of-distribution value estimates (problem #1), this can result in massive gradient norms and subsequent gradient descent procedure using this estimate can diverge rapidly.
Value-gradient aware model learning
To solve the model mismatch problem without introducing new optimization challenges, we argue that a good model loss should have three properties:
- It should minimize the value prediction error under the model. This is the task awareness.
- It should not lead to models predicting next states outside of the data covered region. This ensures stability with function approximation.
- It should be reasonably smooth. This enables easier optimization.
Our key insight is to include the value function into the loss as a measure of the sensitivity of model errors for different data points and observation dimensions. To estimate this, we compute a convex approximation of the value function around each data point by taking its first order Taylor approximation (squared).
This gives us a measure of how sensitive the value function is to distortions in the state space. If the gradient of the value function is low in a specific dimension, the impact of model prediction errors will be relatively small. Conversely, in regions of high gradient, the value function prediction changes rapidly, so the model should measure these dimensions more carefully. In mathematical terms, the gradient allows us to augment the L2 loss in state space by a value function-dependent local regularization for each data point.
\[\hat{\mathcal{L}}_{\hat{V}}=\sum_{\{s_i,a_i,s'_i\}\in\mathcal{D}}{\left(V(s'_i) - \int \hat{P}_\theta(s'|s_i,a_i) (V(s'_i) + (\nabla_s V(s)|_{s'_i})^\intercal (s' - s'_i)) \mathrm{d}s'\right)^2}\] \[=\sum_{\{s_i,a_i,s'_i\}\in\mathcal{D}} {\left(\int \hat{P}_\theta(s'|s_i,a_i) \left((\nabla_s V(s)|_{s'_i})^\intercal(s' - s'_i) \right) \mathrm{d}s'\right)^2}\]We call the loss function the Value Gradient weighted Model loss (VaGraM).
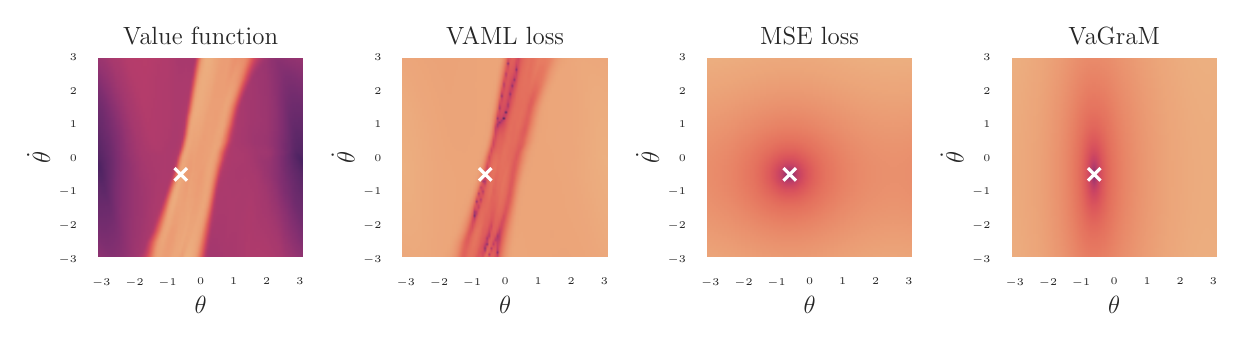 |
A visual comparison of all the discussed value functions. |
Does it actually help in practice?
The theory underlying VaGraM and VAML tells us that a value-aligned loss function should matter most in scenarios where the model is insufficient to capture the full complexity of the environment, or in cases where there are irrelevant dimensions in the state space for the control task. To verify that VaGraM actually increases the performance of a state-of-the-art model based RL algorithm, we conducted two main experiments:
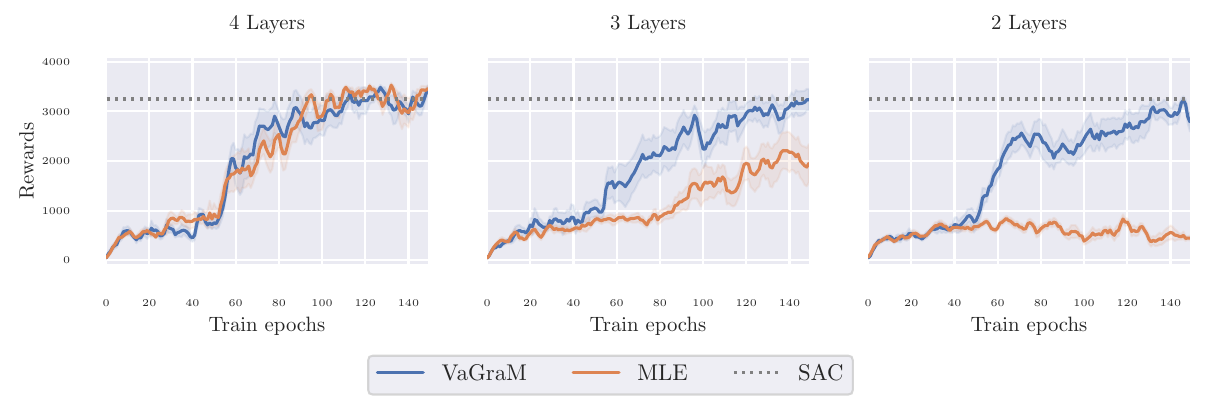
(a) Does VaGraM help when the model doesn’t fit!
We took the popular DM control environment Hopper and Model-based Policy Optimization (MBPO). We replaced the MLE loss in MBPO by VaGraM and gradually decreased the model size to limit its capacity. The performance of the maximum likelihood solution quickly deteriorated as the model grew smaller, while the performance of the VaGraM augmented version stayed stable.
(b) Does VaGraM help when the model is hard to fit due to distracting observations.
We appended superfluous dimensions to the state space following an independent non-linear dynamical system. This proved to be a very challenging environment, and both MBPO and VaGraM dropped in performance quickly with an increasing number of distracting dimensions. Nonetheless, VaGraM managed to stabilize the Hopper and achieve some forward motion when faced with 15 distracting dimensions, while the MLE solution collapsed to the performance of a random policy.
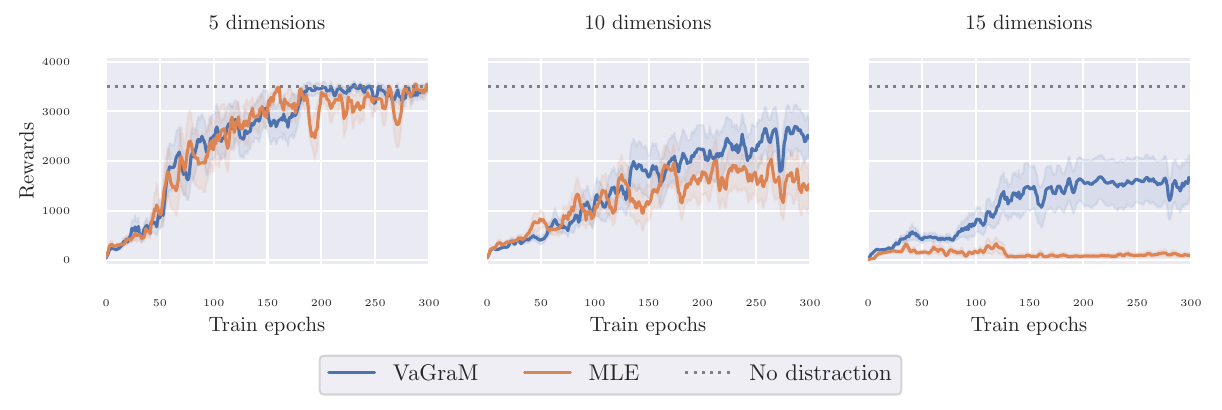
In further experiments we found that VaGraM is able to perform on par with MBPO in all DM control environments, and even outperforms it on the Ant benchmark. We hypothesize that the Ant state space is not perfectly tuned for the control problem, which shows that task-aware losses can achieve better performance even in environments where we previously did not expect the state and observation space to contain superfluous information.
If you want to use and expand VaGraM, the implementation of the core loss function is surprisingly easy and can be included into most deep learning frameworks with only one additional backpropagation pass through the value function network.
Here is the loss function code using the jax library:
def vagram_loss(model_prediction, environment_sample, value_function):
err = model_prediction - environment_sample
_, grad = jax.value_and_grad(value_function)(environment_sample)
return jnp.square(grad * err).sum()